
Menu
Our Blog
Survival Analysis Done Wisely
Survival analysis is one of the most useful and frequently implemented statistic tools in clinical trial analysis, especially in the oncology field. Although the name of this technique may seem to be linked to the analysis of patients’ survival, it is a very versatile technique! Keep reading if you want to learn more about the features and components of this analysis!
By Mercedes Ovejero Bruna
Senior Statistician/Data Scientist at Sermes CRO's Biostatistics & Data Management Unit
Survival analysis is one of the most useful and frequently implemented statistic tools in clinical trial analysis, especially in the oncology field. Although the name of this technique may seem to be linked to the analysis of patients’ survival, it is a very versatile technique! Keep reading if you want to learn more about the features and components of this analysis!
By Mercedes Ovejero Bruna
Senior Statistician/Data Scientist at Sermes CRO's Biostatistics & Data Management Unit

What do we use survival analysis for?
In many clinical studies, one of the main variables that are usually studied is the time that passes until the occurrence of a certain event, for example, until the patient progresses from a pathology, until an adverse event occurs, until they die, etc. But it does not only focus on negative events, but we can also study the time it takes for a patient to respond to a treatment, or even the time passed until the patient is discharged from the hospital.
Basically, what is studied is the period that passes between the start of the (previously established) follow-up and the occurrence of the target event or, failing this, the end of the follow-up period if the mentioned event does not occur. Therefore, the most elementary analyses are composed of two variables that are studied simultaneously:
- Duration: time passed between the established start date and the occurrence of the event or the end of the period. For example, number of weeks passed since the treatment is administered until an event of interest occurs. If the mentioned event does not occur, the end of the period tends to coincide with the end of the study, the end of the follow-up period, etc.
- Event: It is a variable that, in the simplest analyses, has two values: occurrence or non-occurrence of the event of interest. For example, this variable could be the occurrence of a new metastasis, hospital discharge, etc., whose values would be “yes” or “no”.
If the patient, for whatever reason, does not experience the event in the considered timeframe, that would be referred to, in the field of survival analysis, as a “censored case”.
Beware of censoring!
As has been pointed out, the events of interest do not always occur within the stipulated study time. These cases are called censored ones. Now, why can censored cases appear? The origin of these cases does not necessarily have to be something with a negative connotation, but the following are some of the circumstances that determine the definition of censored cases in a practical way:
- The patient has been withdrawn from the study before the end of the follow-up period.
- Follow-up losses. This type of case occurs when the patient cannot be located.
- The patient has had an event other than the event of interest and no further information is available.
- The patient has completed the follow-up period without experiencing the event of interest.
- The patient has been prematurely withdrawn from the study with no record of having experienced the event of interest.
- No information is available if the patient has experienced the event or not. These cases are complicated to analyze given that the patient’s situation relative to the event of interest is uncertain.
In many of these cases, what happens is that no information about the patient is available until the end of the follow-up period, and, therefore, we only thing that is known is that during this observation period the patient hasn’t experienced the event of interest. What is unknown is if the patient has suffered the event at another time.
From a technical point of view, censored cases can be grouped into left-censored, interval-censored, and right-censored cases. An interesting analysis of the types of censored cases can be found at . Although basic survival analysis may not consider the type of censored case we are dealing with, it is important to note that there are advances in the modelling by type of censored case. Reading Turkson et al. (2021) will allow you to get an idea of how to deal with these circumstances.
The (basic) recipe for survival analysis
The basic elements to prepare a good survival analysis can be grouped into:
- Data requirements: The quality of the data is essential in all statistical analysis. If the data we obtain are not of sufficient quality or there are missing data, evidently the survival analysis will be seriously affected. More specifically, the information needed has to do at least with:
- The event: Having information about whether the event has occurred. The definition of the event must be clear, and it must be based on the study’s endpoints. For example, if we are doing an oncology study, the overall survival can be analyzed, in this case, the event would be that the patient has died from any cause in the timeframe of interest.
- The dates: The start date of the interval of interest for all patients must be available, as well as either the end date of the interval if the event has not occurred, or, if it has, the date on which the event occurred. For example, if we are interested in overall survival since the first dose of the treatment was administered, the date on which the treatment was administered, the end date of the study and the date of death (if applicable) must be available.
- The survival function: It indicates the probability of a patient “surviving” beyond a stipulated period. It is important not to lose sight of the fact that the concept of “surviving” is very broad. For example, it could indicate the probability that a patient will recover from their pathology, or that they will progress at a certain time of interest.
- The Kaplan-Meier estimator: The Kaplan-Meier estimator is used in these analyses because, among other elements, it takes into account the censoring of cases. There are other methods other than the Kaplan-Meier method, if you want to learn more, we suggest reading Xu et al. (2012).
What basic results are obtained in a survival analysis?
- Estimation of survival in each timeframe: These results are usually presented on a table, and they show how the patients at risk of suffering the event change over time. It tends to be accompanied by columns indicating the assessed time, the number of patients at risk, the number of accumulated events, the probability of survival along with its confidence interval, and the standard estimation error.
- Estimation of mean, median and percentiles of survival times: This summary table allows us to visualize the results for the group of patients of interest, in addition, it can be broken down according to variables such as randomization group, so that we can study not only whether there are differences between the groups, but also, by adding an inferential analysis, it is possible to see whether they are significant.
- The survival graph: It is a graph that, in a very visual way, allows us to check how the probability of the event varies over time. In the example below, we can see that the probability drops quite steeply between time 0 and 150 days. In addition, we can also see when the censored cases, marked with | in the graph, appear.
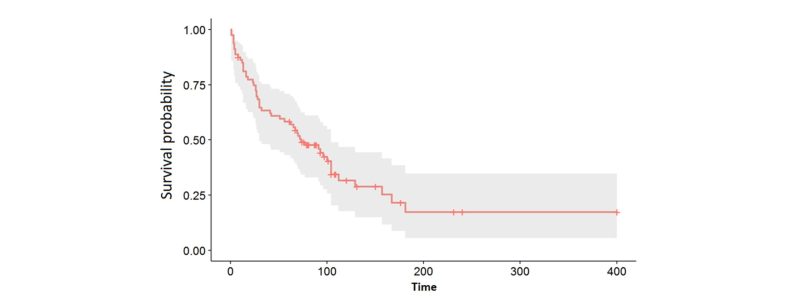
- Cumulated risk function: This function shows the probability that a patient being observed at time “t” will experience the event of interest at that time. It allows us to answer questions such as “what is the probability that a patient who has been treated with an experimental treatment will die after 6 months (assuming he have survived until that time)?”. An example of this graph is presented below.
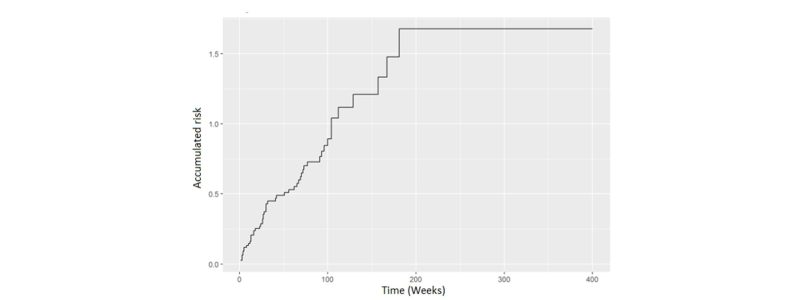
While the survival function focuses on reporting the “non-occurrence” of the event (for example, the patient has not died), the risk function focuses on the “occurrence” of the event. This is very interesting because it allows us to pose answers to questions such as, for example, “at what point am I going to have a ‘spike’ in hospital discharges?” Curiously enough, this function is hardly ever reported, and, as we have seen, it provides more interesting information in the area of clinical studies.
Challenges of these analyses
In conclusion, survival analyses allow to study the time passed until the occurrence of a certain event. Although basic analyses are very intuitive to interpret, they can become something very complex. This makes them a real challenge in contexts such as:
- The need to incorporate different covariates: One of the possible solutions in this case is modeling by Cox regression (a review of this model can be found in Fox and Weisberg, 2018). These analyses make it possible to study the dependence of survival time considering a series of predictor variables, such as the randomization group, patients’ age, the severity of the pathology, etc.
- When the event is time-dependent: We may be studying an event of interest that is much more likely to occur at the start of the follow-up period than at the end of the study when considering certain risk factors. In this situation, we should bear in mind that the Cox proportional hazards model may require some extensions (Kleinbaum and Klein, 2011).
- A patient may experience more than one event: This is very common when, for example, we are studying relapses, since a patient may have more than one (Baethge and Schlattmann, 2004). In these cases, the biases associated with survival-dependent censoring must be corrected (Gómez, 2012; Ruth et al., 2022).
- Large volumes of data: Sometimes, the analysis incorporates a great number of variables. When the number of variables is very large, the analysis faces the challenge of high dimensionality. The use of machine learning tools becomes then an optimal alternative (an example of such applications can be found in Gong et al., 2018).
As open-source software recommendations, the R packages survival and survminer, as well as Python’s scikit-survival, are versatile tools that allow for the elaboration of both basic as well as more advanced survival analysis.
References
Baethge, C., & Schlattmann, P. (2004). A survival analysis for recurrent events in psychiatric research. Bipolar Disorders, 6(2), 115-121.
Fox, J., & Weisberg, S. (2002). Cox proportional-hazards regression for survival data. An R and S-PLUS companion to applied regression, 2002.
Gómez, G., & Serrat, C. (2014). Correcting the bias due to dependent censoring of the survival estimator by conditioning. Statistics, 48(2), 295-314.
Gong, X., Hu, M., & Zhao, L. (2018). Big data toolsets to pharmacometrics: application of machine learning for time‐to‐event analysis. Clinical and translational science, 11(3), 305-311.
Kassambara, A., Kosinski, M., & Biecek, P. (2021). survminer: Drawing Survival Curves using ‘ggplot2’. R package version 0.4.9, https://CRAN.R-project.org/package=survminer.
Kleinbaum, D. G., & Klein, M. (2012). Extension of the Cox proportional hazards model for time-dependent variables. In Survival analysis (pp. 241-288). Springer, New York, NY.
Pölsterl, S. (2020). scikit-survival: A Library for Time-to-Event Analysis Built on Top of scikit-learn. Journal of Machine Learning Research, 21(212), 1–6.
Prinja, S., Gupta, N., & Verma, R. (2010). Censoring in clinical trials: review of survival analysis techniques. Indian journal of community medicine: official publication of Indian Association of Preventive & Social Medicine, 35(2), 217.
Ruth, D. M., Wood, N. L., & VanDerwerken, D. N. (2022). Fully nonparametric survival analysis in the presence of time-dependent covariates and dependent censoring. Journal of Applied Statistics, 1-15.
Therneau, T. (2022). A Package for Survival Analysis in R. R package version 3.3-1, https://CRAN.R-project.org/package=survival.
Turkson, A. J., Ayiah-Mensah, F., & Nimoh, V. (2021). Handling Censoring and Censored Data in Survival Analysis: A Standalone Systematic Literature Review. International Journal of Mathematics and Mathematical Sciences, 2021.
Xu, S., Shetterly, S., Powers, D., Raebel, M. A., Tsai, T. T., Ho, P. M., & Magid, D. (2012). Extension of Kaplan-Meier methods in observational studies with time-varying treatment. Value in Health, 15(1), 167-174.
Certifications:














